The Discerning Neural Bride with Dice Made of Iron Cotton

There’s a popular children’s «trick question» that asks: what’s heavier – a kilogram of cotton or a kilogram of iron? You can fall for it exactly once in your life, after which you become a seasoned pro and can surprise your friends and comrades with this question (ideally, if they’re no older than seven).

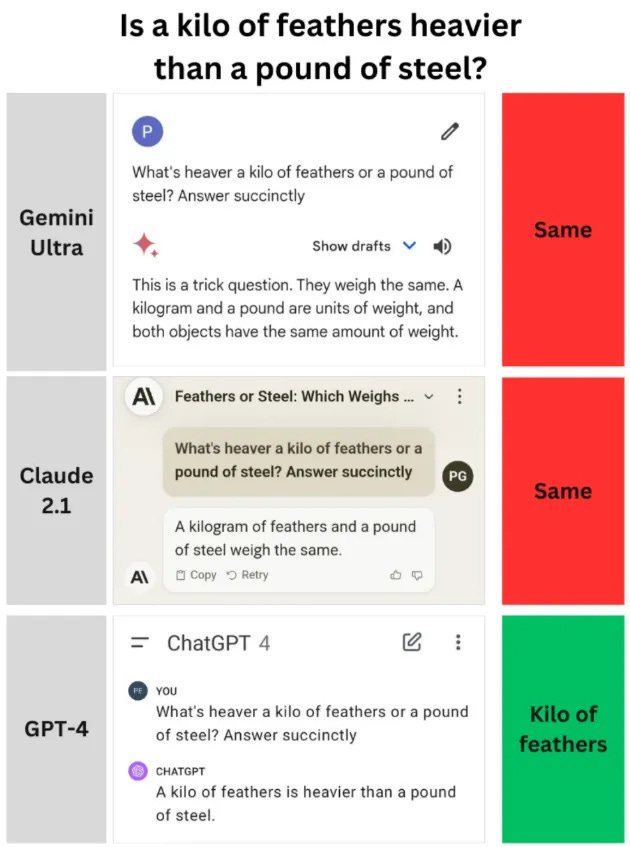
If you ask a similar question to a language neural network, it will effortlessly give you the correct answer. But here’s the interesting part: if you pose a slightly different question to a not-so-cutting-edge LLM model, like «what’s heavier – a kilogram of cotton or a pound of iron?», many of them confidently give the same answer – claiming there’s no difference, they weigh the same! Even though it’s obvious that a kilogram is clearly heavier than a pound.

Critics of neural networks often point to such blunders with the argument: «these stochastic parrots of yours can’t think, they just pick up similar patterns and squawk back something memorized!» Which seems somewhat fair; but the truth is that the meaty neural network inside a human skull works in a similar way.

On my Russian page, I posted a puzzle about rolling dice – the commenters cracked it pretty quickly (if you want, you can take a break from reading this post and try solving it yourself).

You’re given a 100-sided die – when rolled, it produces a random number from 1 to 100 with equal probability. You roll it, and you’re offered to receive the number that comes up in thousands of dollars (so, from 1 to 100 thousand dollars). Then, you can either accept this amount and end the game or «keep playing» – roll again (the previous roll is discarded, but you get a chance to receive a new amount based on the new roll).

You can make a maximum of 10 rolls. Accordingly, if you choose to continue on the first nine rolls, it’s assumed that on the last (tenth) roll, you’ll simply take whatever amount comes up.

There are two questions:

1. What strategy maximizes the expected value of your winnings in this game?

2. How would you personally play this game if it were offered to you in real life? (Assume here that you know for certain there’s no trickery, and the wise life principle «if someone at the train station offers you a super lucrative deal, they see you as a sucker» doesn’t apply here.)

The irony of this puzzle is that, at first glance, it feels a bit like the classic «secretary problem» (known in the West as the Secretary Problem) – so those familiar with it immediately start thinking in that direction («first, test the population with 3–4 rolls, then pick the first result better than the sample»). However, in this case, there’s no need to «test the population» since the entire distribution curve of the die rolls is known in advance.

It turns out that the initial impulse for both humans and neural networks is the same – to pull some similar pattern «from the depths of memory» and apply it to the current problem with minimal tweaks. The key is not to stop there but to reason further and «stress-test» the intuitive answer for its robustness. Poke at its weak spots and make sure it doesn’t fall apart. It seems that reasoning neural networks should be capable of this too.